Картинки из квадратов \ Арифметика "на квадратах" \ Разное \ Античная арифметика \ Реакция на кризис: "геометрическая алгебра" \ Боковые и диагональные числа \
 

7.3.1.11.2.1. Боковые и диагональные числа
по версии Б. Л. ван дер Вардена ©

 
Платон в "Государстве" (546 С) называет число 7 "рациональной диагональю", соответствующей стороне 5.
В пояснение к этому Прокл дает следующее определение "боковых и диагональных чисел", которое он приписывает пифагорейцам и с которыми мы также встречаемся у Теона Смирнского и у Ямвлиха:
"Единица, как начало всех чисел, в потенции является и стороной, и диагональю.
В таком случае возьмем две единицы: одна будет боковой, а другая — диагональной.
Теперь образуем новую сторону, прибавив к единице-стороне единицу-диагональ, и новую диагональ, прибавив к единице-диагонали дважды единицу-сторону".
Таким образом получается боковое число 2 и диагональное число 3. После этого с полученными числами поступают подобным же образом:
2 + 3 = 5,    (22) + 3 = 7
и т. д., следуя формуле
  an+1 = an + dn,    dn+1 = 2an + dn. ( 1 )
Название боковых и диагональных чисел объясняется тем, что отношение andn представляет приближенное значение отношения стороны квадрата к его диагонали.
Это вытекает из тождества
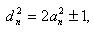
  ( 2 )
которое, согласно Проклу (комментарий к "Государству" Платона, II, главы 23 и 27) доказывается при помощи Предложения 10 из II книги Начал.
Отсюда мы видим, что пифагорейцы, в сущности, знали принцип полной индукции и что они применяли "геометрическую алгебру" к задачам из теории чисел.
Но как они пришли к рекуррентным формулам ( 1 )? Полагаю, что это произошло следующим образом.
Для определения общей наибольшей меры двух взаимоизмеримых величин a и b греческая математика знает способ попеременного вычитания (antanairesis): меньшую величину, например, a, вычитают из большей, так что получаются две новые величины a и (b - a), затем снова меньшую вычитают из большей и т. д.
Если существует общая мера, то этот процесс неизбежно приведет к двум равным величинам c = d, каждая из которых и есть общая наибольшая мера.
В VII книге Начал этот метод применяется для нахождения общего наибольшего делителя чисел, а в начале книги X — для произвольных величин, чтобы установить, имеется ли у них общая мера и если да, то какова она.
Однако, если применить этот способ к двум несоизмеримым величинам, то процесс становится бесконечным.
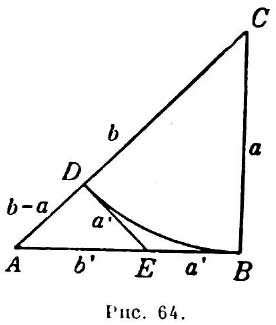
Если, например, a есть сторона, а b — диагональ квадрата, то a можно один раз отнять от b (рис. 64).
Остаток b - a = AD = DE = EB = a' можно снова отнять от
a = AB; в остатке получится b' = AE.
Теперь a' и b' опять представляют сторону и диагональ меньшего квадрата, и из
следует:
Формулы (4) уже имеют тот же вид, что рекуррентные формулы (1). Если мы продолжим процесс повторяющегося вычитания, то опять получим еще меньшие сторону и диагональ, a'' и b''.
Если мы дойдем до того, что разность между a''' и b''' станет чрезвычайно малой, и остановимся на приближении a''' = b''', выбрав a''' в качестве единицы длины, тогда a'' и b'', a' и b' и, наконец, a и b по формуле (4) будут представлены в виде ряда последовательных боковых и диагональных чисел.
Задача о получении в рациональных числах приближенного значения для отношения диагонали квадрата к его стороне была поставлена и решена вавилонянами.
Но для этой старой проблемы пифагорейцы сделали бесконечно больше, чем вавилоняне.
Они нашли целый ряд приближений неограниченно возрастающей точности, а кроме того, создали научную теорию этих приближений и доказали общее предложение (2) при помощи полной индукции.
Снова и снова мы видим, какие великолепные теоретики в области чисел были в пифагорейской школе.
  К началу данной страницы  
Картинки из квадратов \ Арифметика "на квадратах" \ Разное \ Античная арифметика \ Реакция на кризис: "геометрическая алгебра" \ Боковые и диагональные числа \