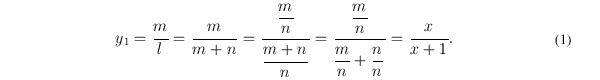Начало см. здесь.

1. О рациональных отношениях и струнах
в музыкальной теории

Концепция рациональных отношений стояла у истоков (западной) музыкальной теории. Б. Л. ван дер Варден пишет: "Исходя из упомянутых ... повседневных наблюдений о влиянии на высоту тона натяжения, длины струны или звучащего столба воздуха, а может быть также и под влиянием вавилонских теорий, Пифагор пришел к мысли о сопоставлении тонов с числами, а консонансов — с числовыми отношениями".

Примем во внимание также мнение классика Римана: Следует ли поэтому начинать историю музыки только с Рождества Христова? Нет, тогда была бы пропущена эпоха, из которой мы хотя и не имеем ни одной мелодии, но имеем зато известное число теоретических сочинений, по которым можно составить понятие о высоком состоянии музыкального искусства в те времена. Такова эпоха процветания древней Греции, в ней коренится вся музыка средних веков, а музыкальная теория древних греков составляет и в настоящее время основу научного определения нашего искусства.

Определенное значение концепции рациональных отношений придает Ю. Н. Холопов: В науке истина теории должна быть показана "во весь рост", в свою полную величину, простирающуюся от эстетики художественного явления (соответственно также техники композиции), от каллистики, философии, социологии, мировоззренческих категорий через представления психологии восприятия, через физиологию музыкального ощущения, физику реального звучания (акустику, "природу") вплоть до бесстрастной красоты числовых отношений. Автор не считает, что "во всяком учении столько науки, сколько в нем математики", однако ясно, что в ряде аспектов науки о гармонии (в особенности на низшем, элементарном уровне) оперирование числовыми структурами закономерно и необходимо привходит в естественный язык научной теории музыки.

Очень часто в музыкальной теории понятие рациональных отношений возникает в контексте определенных манипуляций со струнами, под которыми понимаются, в сущности, просто некоторые геометрические отрезки на Евклидовой плоскости. См., например, у Форстера.

Люсьен Шевалье пишет о теории Рамо: "... Так как трудно измерить частоту колебаний, а, с другой стороны, соотношения между числами колебаний обратно пропорциональны длинам струны, которые легче измерять, Рамо применяет числовые обозначения к струнам, что, конечно, ни в чем не может повлиять на конечный результат. Таким образом, ... он на первых страницах трактата 1722 г. выписывает следующую цитату из Декарта: "Звук относится к звуку так же, как струна к струне". Это — краеугольный камень постройки, идет ли речь о первой или второй системе Рамо".

Далее Л. Шевалье продолжает: "Что можно сделать из струны, желая извлечь из нее нечто новое? Делить ее."

Я постулирую существование элементарных действий музыкально-теоретического интеллекта, производимых им во время такого (мысленного) деления струны на части и намерен аксиоматизировать свойства этих действий в первую очередь. Называть я их буду: "элементарный инь-конструктор V" и "элементарный ян-конструктор H". К неформальному пояснению их музыкально - теоретического смысла я сейчас и приступаю.

2. Неформальное пояснение музыкально - теоретического смысла элементарного инь-конструктора V
и элементарного ян-конструктора H

Представим себе некоторую струну:

Пусть ее длина равна :

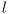
Предположим, что эта струна разделена на две части с длинами m и n, соответственно, в некотором рациональном отношении :

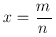
(очевидно, что )

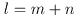
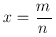
Всегда, когда имеет место указанное выше деление струны в отношении , будет однозначно определено также и другое рациональное отношение длин струн, а именно, отношение

Таким образом, между переменными y₁ и x существует некоторая функциональная зависимость, которую мы будем обозначать символом V и которую будем формально записывать в виде:

Далее зту функциональную зависимость (или унарную операцию), соответствующую унарному функциональному символу V, будем называть элементарным ян-конструктором рациональных отношений (или элементарным ян-конструктором рациональных музыкальных интервалов).

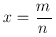
Аналогично, всегда, когда имеет место указанное выше деление струны в отношении , будет однозначно определено также и еще одно рациональное отношение длин струн, а именно, отношение

Таким образом, между переменными y₂ и x существует некоторая функциональная зависимость, которую мы будем обозначать символом H и которую будем формально записывать в виде:

Далее зту функциональную зависимость (или унарную операцию), соответствующую унарному функциональному символу H, будем называть элементарным инь-конструктором рациональных отношений (или элементарным инь-конструктором рациональных музыкальных интервалов).

Неформальное обсуждение инь- и ян- философии в контексте некоторой системы рациональных отношений см. здесь. Название "конструктор" для элементарных инь- и ян- конструкторов музыкальных интервалов заимствовано из терминологии логического программирования.

3. Пример: деление струны пополам

Пусть исходная струна:

разделена пополам:

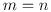
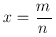
В этом случае и отношение есть отношение равенства, которому соответствует музыкальный интервал унисона (будем обозначать его символом u).

Применение к интервалу унисона u элементарного ян-конструктора V даст интервал повышающей октавы, который получит обозначение V(u).

Применение к интервалу унисона u элементарного инь-конструктора H даст интервал понижающей октавы, который получит обозначение H(u).

Неформальное определение понижающих и повышающих рациональных музыкальных интервалов приведено у Немировского.

4. Калькулятор для игр с конструкторами V и H

По этому адресу приведен калькулятор для игр с конструкторами V и H. Там же приведена и некоторая электротехническая их интерпретация.