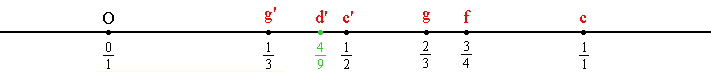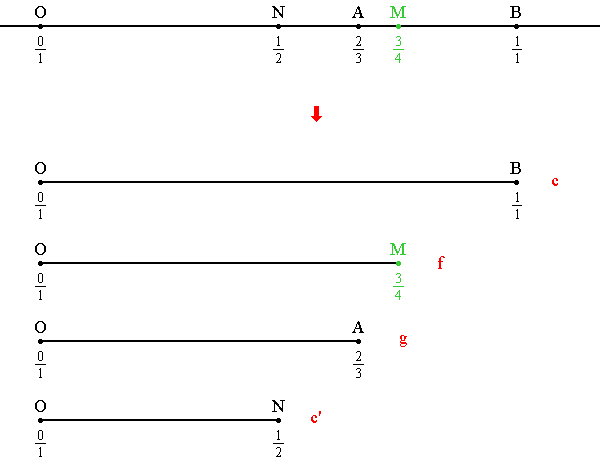
Объяснение этого звукоряда у Немировского см. здесь. Знак вопроса, который там у него стоял, замещается струной f, длина которой является четвертой гармонической для тройки уже известных струн c, g и c'. Другими словами, точки N, A, M, B на прямой, изображенной ниже, образуют гармоническую четверку точек. Саму эту прямую мы можем рассматривать как некоторую прямую, с выбранной на ней системой координат. Таким образом числа, приписанные точкам N, A, M, B, являются их координатами в этой выбранной системе координат (см. соответствующие определения, например, у Александрова П. С.)

Указанные точки на нашей "числовой прямой" естественным образом порождают четверку отрезков, которые, будучи интерпретированы как струны соответствующей длины, и образуют "звукоряд Орфея". В соответствии с определениями Пифагора, струны с указанными соотношениями длин, дадут именно те звуки, которые нужно.

Гармонию N = 1/2, A = 2/3, M = 3/4, B = 1/1 мы можем увидеть на третьем уровне Дерева. Именно эта гармония использовалась для объяснения работы калькулятора на Арбузе: http://forum.arbuz.uz/index.php?showtopic=2192
(пост от 12 сен 2008, 15:22 на указанной странице). Копию этой страницы см. здесь.

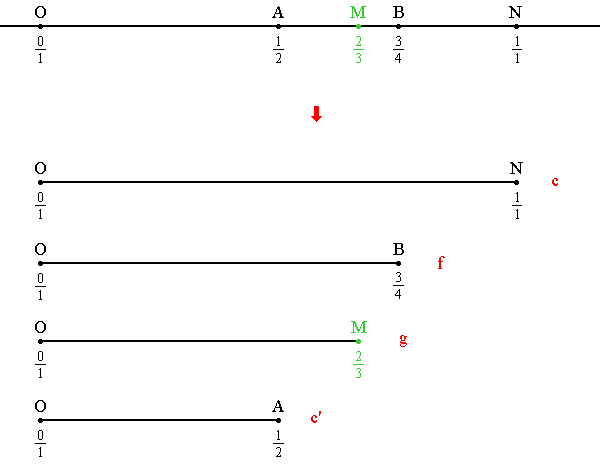
С другой стороны, если в качестве "исходных" заданы струны c, f и c', то недостающая до Орфеева звукоряда струна g снова может быть получена как четвертая гармоническая к трем уже заданным. Это является расшифровкой того факта, что на нашей "числовой прямой" точка M = 2/3 делит внутренним образом отрезок с концами A = 1/2 и B = 3/4 в том же самом отношении, в каком точка N = 1/1 делит тот же самый отрезок внешним образом. Значит, согласно определению, точки M и N делят гармонически отрезок AB, или, что тоже самое, точка M является четвертой гармонической к тройке точек A, B, N.

Как и ранее, указанные точки A, M, B, N на нашей "числовой прямой" естественным образом порождают четверку отрезков, которые, будучи интерпретированы как струны соответствующей длины, и образуют "звукоряд Орфея". В соответствии с определениями Пифагора, струны с указанными соотношениями длин, дадут именно те звуки, которые нужно.

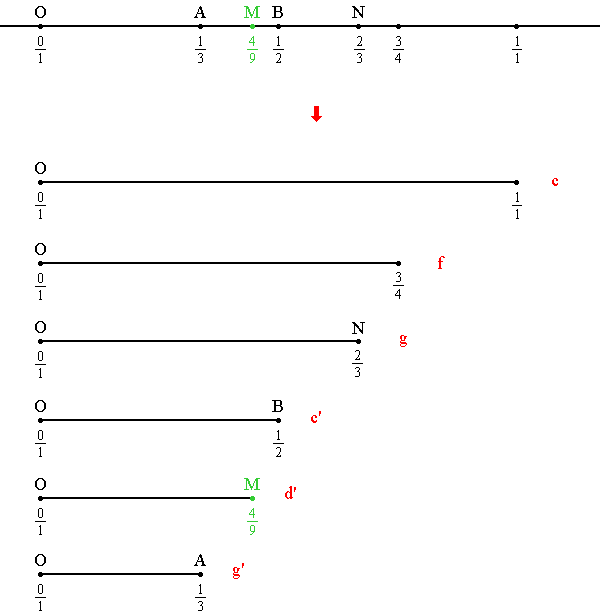
Понятно, что и дальнейшие струны пифагорейского звукоряда могут быть построены путем систематического применения одной и той же операции: построения четвертой гармонической к некоторой уже построенной ранее тройке струн. Например, струна, отвечающая звуку d', может быть построена как четвертая гармоническая к уже построенной ранее тройке струн, ассоциированных со звуками g', c' и g.

Построение такой системы "струн" можно интерпретировать как построение точек "числовой прямой":

Причем это можно сделать таким образом, каким осуществляется построение точек проективной шкалы у Ефимова (по Клейну). Ну чем не монохорд получился?!

Продолжение см. здесь.