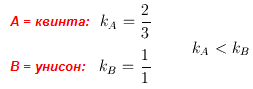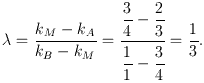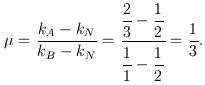Рассмотрим множество рациональных лучей, линейно упорядоченное по величине угловых коэффициентов лучей. Следуя обычным определениям мы можем говорить об, например, открытых интервалах в этом линейном порядке. Чтобы не путаться при этом с рациональными музыкальными интервалами, которые, как мы будем считать, представляются рациональными лучами, слово "интервал" в этом первом случае будем брать в кавычки.

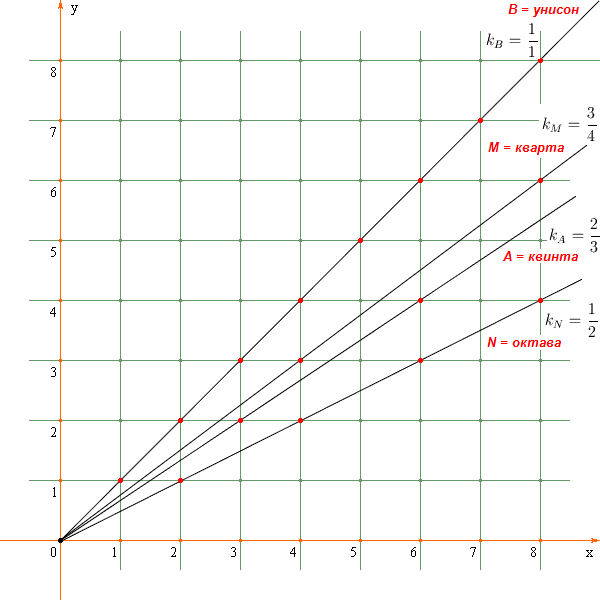
1. Пример гармонической четверки лучей, отвечающих унисону и понижающим квинте, кварте и октаве

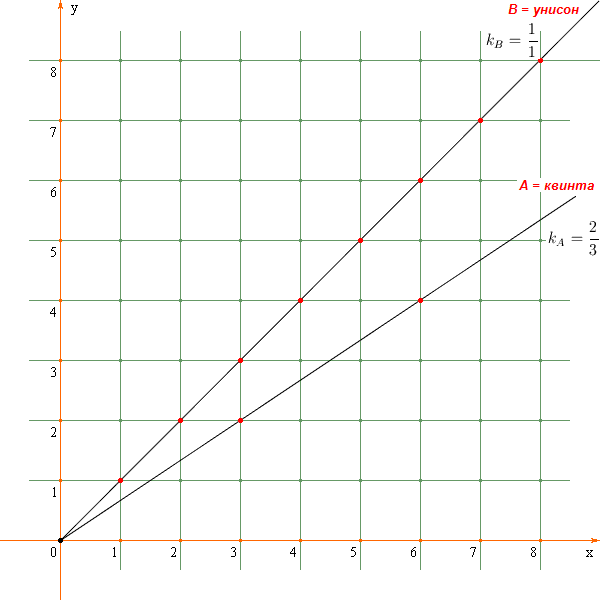
Определение повышающих и понижающих музыкальных интервалов, представленных лучами, в зависимости от величины углового коэффициента лучей, см. здесь. Лучевой "интервал" с меньшим концом в виде луча A (квинта) и большим концом в виде луча B (унисон) изображен ниже. Разумеется, на приведенном ниже рисунке изображен не сам лучевой "интервал", а только лишь его концы.

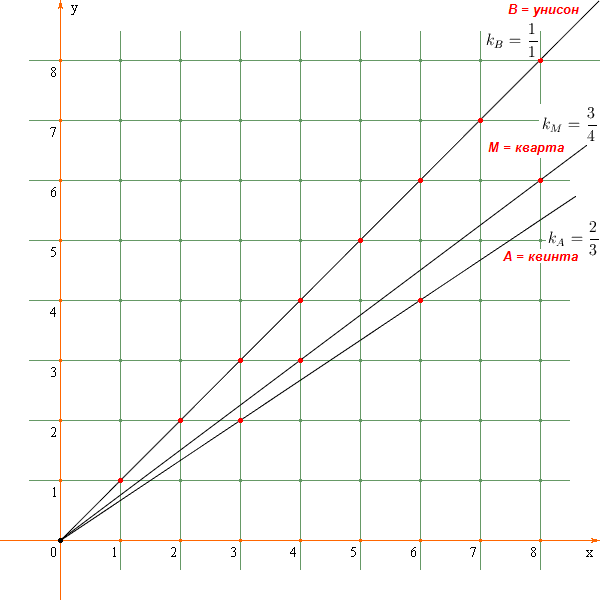
Лучевой "интервал" с меньшим концом в виде луча A и большим концом в виде луча B будем обозначать как (A, B). Луч M (кварта) с угловым коэффициентом k_M делит этот лучевой "интервал" внутренним образом в отношении:

Деление отрезка в некотором отношении внутренним образом в случае числовой прямой см. у Адамара здесь. Далее, луч N (октава) с угловым коэффициентом k_N делит лучевой "интервал" (A, B) внешним образом в отношении:

Деление отрезка в некотором отношении внешним образом в случае числовой прямой см. у Адамара здесь. Поскольку у нас получилось, что

то мы можем утверждать, что лучи M и N являются гармонически сопряженными относительно лучей A и B или что лучи M и N гармонически делят лучевой "интервал" (A, B). Гармоническое деление отрезка в случае числовой прямой см. у Адамара здесь.

По другому можно еще сказать, что четверка лучей N, A, M, B образует гармоническую четверку лучей.

В принципе, все сказанное здесь по поводу гармонической сопряженности согласовано с определением более общего сложного отношения четырех лучей пучка в проективной геометрии (как, например, у Н. В. Ефимова здесь).

2. Интерпретация на Дереве Штерна - Броко

Мы можем считать, что вершины Дерева Штерна - Броко (см. о нем также здесь) помечены угловыми коэффициентами рациональных лучей. Тогда сам рост Дерева может интерпретироваться как последовательное применение операции построения луча, являющегося "четвертым гармоническим" к некоторой уже построенной тройке рациональных лучей.

Для проведения экспериментов в этом направлении может быть адаптирован калькулятор, ранее созданный для работы с рациональными точками числовой прямой. В частности, для иллюстрации разобранного выше примера гармонической четверки лучей нужно ввести в поле "исходное число" калькулятора значения: числитель = 3 и знаменатель = 4. Результаты работы калькулятора должны выглядеть следующим образом: