Начало см. здесь и здесь.

В математике важное значение имеет идея взаимно однозначного соответствия. Установление такого соответствия позволяет, в частности, заменять одну систему объектов некоторой другой системой объектов, которая в некотором смысле оказывается эквивалентной исходной системе и с которой по какой-то причине оказывается более удобно работать. Суть дела на интуитивном уровне хорошо проясняется известным сравнением шахматных фигур с кусочками угля.

В частности, мы можем установить взаимно однозначное соответствие между точками первого квадранта координатной плоскости, не лежащими на осях координат, и их координатными прямоугольниками. Идея координатного прямоугольника данной точки очень подробно объясняется у Делоне-Райкова.

У них, правда, рассматривается более общий случай координатного параллелограмма данной точки, но совершенно ясно, каким образом адаптировать эту конструкцию для случая декартовой прямоугольной системы координат. Соответствующая терминология приводится и у Делоне-Райкова в отдельном замечании.

В случае построенного ранее Золотого Прямоугольника ARVU:

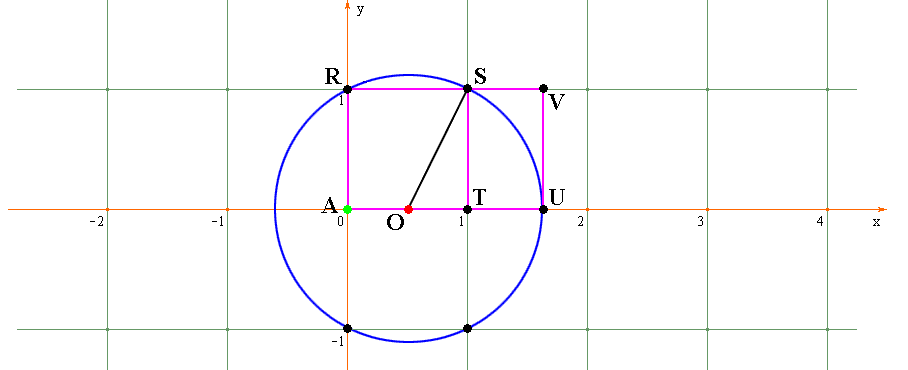
мы можем заменить этот прямоугольник одной единственной точкой V, по которой этот прямоугольник однозначно восстанавливается (очевидно, прямоугольник ARVU является координатным прямоугольником точки V в смысле приведенных выше определений).

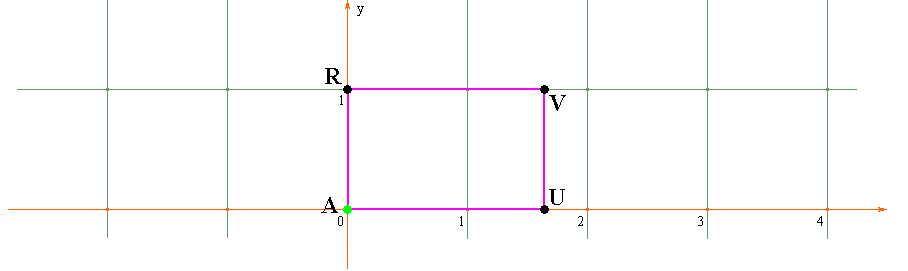
По этой единственной точке V, прямоугольник ARVU однозначно восстанавливается:

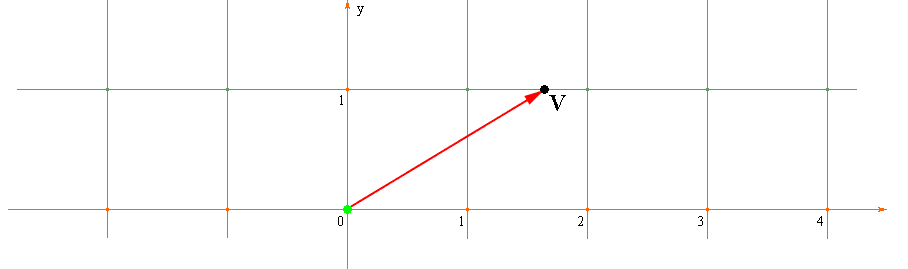
2. Взаимно однозначное соответствие с радиус-векторами

Мы можем пойти дальше и установить взаимно однозначное соответствие между координатными прямоугольниками точек первого квадранта, не лежащих на координатных осях, и радиус-векторами. Это позволит нам (в духе сформулированной выше методологии) заменить прямоугольники радиус-векторами.

В частности, мы можем заменить построенный ранее Золотой Прямоугольник ARVU радиус-вектором точки V:

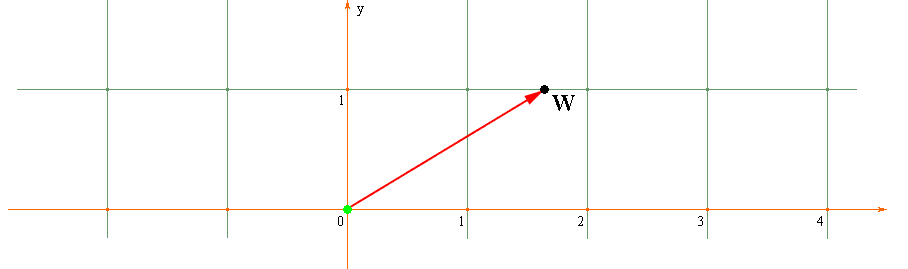
Теперь мы желаем показать, что применение к этому радиус-вектору в определенном порядке моих любимых операторов V и H снова дает радиус вектор, отвечающий Золотому Прямоугольнику. Чтобы не путаться при этом с обозначениями точек и операторов, мы переобозначим интересующую нас исходную точку буквой W:

С геометрической точки зрения операторы V и H представляют собой некоторые преобразование сдвига; объяснение действия оператора H приведено, например, в учебнике Акивиса и Гольдберга (пример з) при k = 1). Поскольку при этом преобразовании конец радиус - вектора сдвигается параллельно оси абсцисс ("горизонтальной оси"), то преобразование мы обозначаем буквой H (от слова "Horizontal"); аналогично и с буквой V (от слова "Vertical").

О преобразованиях сдвига можно посмотреть также у Делоне-Райкова и у Яглома-Ашкинузе.

Продолжение см. здесь.