Мы можем определить Q+ как систему следующего вида:

Q+ = < Q+, , , >,

где Q+ есть множество всех положительных рациональных чисел;

есть некоторая бинарная операция на множестве Q+, именуемая "операцией горизонтального сложения рациональных чисел", которая определяется следующим образом: xy = x + y;

есть некоторая бинарная операция на множестве Q+, именуемая "операцией вертикального сложения рациональных чисел", которая определяется следующим образом: ;

 есть некоторая унарная операция на множестве Q+, именуемая "операцией обращения рациональных чисел", которая определяется следующим образом: .

Система R+ определяется абсолютно точно так же, как и система Q+; единственное отличие заключается в том, что в качестве множества-носителя у системы R+ выступает множество R+ всех положительных вещественных чисел.

Некоторое обсуждение систем Q+ (R+) было предпринято в http://dxdy.ru/topic16277.html
(с акцентом на рассмотрение феномена "двойственности", имеющегося в этих системах).

Для систем Q+ (R+) являются, очевидно, справедливыми следующие два утверждения:

(i)  существует элемент, удовлетворяющий условию ;

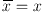
(ii)  такой элемент является единственным.

Положив этому элементу естественное имя "1", мы можем определить две двойственные друг по отношению к другу унарные операции: H(x) = x1 и V(x) = x1.

При помощи этих двух унарных операций H и V, примененных в различных комбинациях к 1, мы, как можно показать, можем получить все положительные рациональные числа, причем разным комбинациям будут соответствовать разные числа. Например, V(H(H(1))) = 3/4, что можно проверить прямым вычислением в соответствии с определением операций H и V.

Операции V и H естественным образом порождают одно из двух замечательных Деревьев по следующим правилам:

(i)  корень дерева помечаем числом 1;

(ii)  если некоторая вершина дерева помечена положительным рациональным числом x, то левого сына этой вершины помечаем числом V(x), а правого сына этой вершины помечаем числом H(x).

Указанным способом порождается "поверхностное дерево" (известное также как "Calkin-Wilf Tree"; на приведенном рисунке оно дорощено до четвертого уровня). Второе из двух замечательных Деревьев — "Stern-Brocot Tree" — порождается при помощи операций V и H несколько более замысловатым способом (подробности см. на http://dxdy.ru/topic16277-60.html).

Смысл того, чтобы обозначать определенные выше унарные операции именно символами "V" и "H", заключается в желании связать их со словами "Vertical" и "Horizontal". Такое желание можно мотивировать визуальными образами, сопровождающими работу древнего алгоритма Антанаиресис, который, по большому счету, и является отцом обоих Деревьев.

Система Q+ является фактор-алгеброй алгебраической системы RA_standard по отношению эквивалентности (мы назвали его "отношением пропорциональности"); это отношение, как нетрудно показать, является некоторой конгруэнцией алгебраической системы RA_standard.

Определение общеалгебраического понятия "конгруэнция" см., например, здесь
(в разделе Universal algebra): http://en.wikipedia.org/wiki/Congruence_relation.
В фактор-алгебре Q+ операции и становятся уже всюду определенными операциями, так что нам не нужно будет заморачиваться с отношениями пресуппозиции и .