Начало см. здесь и здесь.

Антанаиресис является одним из столпов античной математики. В той или иной степени его влияние ощущается практически во всех сколько-нибудь значимых математических конструкциях того времени. Например, в тех, которые были связаны с "первым научным кризисом". Но не только в них, конечно.

Более того, Антанаиресис представляет собой яркий пример того, что смогло выжить (в том смысле, как об этом пишут Кац - Улам). И не только смогло выжить, но и смогло "положить начало развитию наиболее плодотворных математических теорий". Например, теории цепных дробей.

Таким образом математическую конструкцию, примененную в самом первом предложении самого первого учебника по теории чисел, действительно можно в значительной степени считать основанием этой теории.

В своей "базовой" версии Антанаиресис формулируется для отрезков прямых
a и b  — т. е. для некоторых одномерных объектов. Однако способ мышления, принятый в "геометрической алгебре", позволяет рассмотреть для любых двух отрезков также и "заключенный между ними прямоугольник" (типичный пример подобных рассуждений можно найти в евклидовом Предложении II, 11, посвященном "золотому сечению").

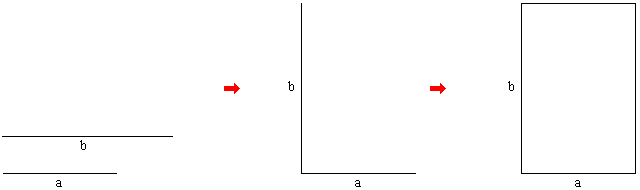
После этого исходная задача часто может быть переформулирована в терминах манипуляций с прямоугольниками и квадратами — т. е. с некоторыми двумерными объектами. Следующий рисунок поясняет эту методологию конкретно для Антанаиресиса.

Сначала имеются два отрезка a и b, для которых нужно найти наибольшую общую меру. Один из отрезков (например, b) поворачиваем на 90 градусов и пристыковываем к отрезку a как показано на рисунке. Затем естественным образом дополняем полученную конфигурацию до прямоугольника со сторонами a и b.

Тогда самый первый шаг алгоритма Антанаиресис, о котором пишет в приведенной выше цитате Б. Л. ван дер Варден, можно промоделировать путем вписывания квадрата в построенный прямоугольник.

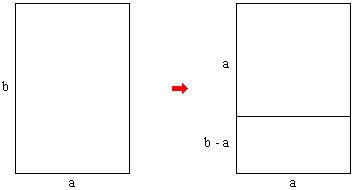
Полученный после вписывания квадрата "остаточный прямоугольник" представляет новую пару величин a и (b - a), к которой применяется следующий шаг алгоритма и т. д.

Впервые я познакомился с этой идеей в книге Н. Н. Воробьева, после чего запрограммировал "визуализатор Антанаиресиса". Интересно отметить, что в такой "квадратной" трактовке Антанаиресис оказывается тесно связанным с квадратными уравнениями "гиперболического типа" (по античной классификации).

Еще одной яркой геометрической метафорой для алгоритма Антанаиресис является "звездное небо" в изложении Феликса Клейна. На самом деле обе эти метафоры (с прямоугольником, разбиваемым на квадраты, и с "небом") тесным и плодотворным образом связаны друг с другом, как будет показано далее.

Следует отметить также, что в античности существовали и другие методы отыскания наибольшей общей меры двух величин, отличные от Антанаиресиса. Описание одного из таких методов приведено в самом начале статьи Радемахера - Теплица о "фантастическом открытии".